Moodle
Αλλαγή μεγέθους γραμματοσειράς
 
ΚΕΦΑΛΑΙΟ 1ο: ΜΗΧΑΝΙΚΕΣ ΤΑΛΑΝΤΩΣΕΙΣ
ΕΝΟΤΗΤΑ 1.1: ΠΕΡΙΟΔΙΚΟ ΦΑΙΝΟΜΕΝΟ - ΑΠΛΗ ΑΡΜΟΝΙΚΗ ΤΑΛΑΝΤΩΣΗ (ΚΙΝΗΜΑΤΙΚΗ ΚΑΙ ΔΥΝΑΜΙΚΗ ΠΡΟΣΕΓΓΙΣΗ)



  • Οι μαθητές πρέπει να είναι ικανοί:

    • Να αναφέρουν περιοδικά φαινόμενα και περιοδικές κινήσεις από το φυσικό και το τεχνολογικό περιβάλλον με κριτήριο την έννοια της επαναληψιμότητάς τους σε συγκεκριμένο χρονικό διάστημα.
    • Να διασυνδέουν τις έννοιες ‘ταλάντωση’, ‘γραμμική ταλάντωση’, ‘απλή αρμονική ταλάντωση’ με την έννοια της ‘περιοδικής κίνησης’.
    • Να αναγνωρίζουν, χρησιμοποιώντας παραδείγματα, τις διαφορές ανάμεσα στην ‘ταλάντωση’, τη ‘γραμμική ταλάντωση’ και την ‘απλή αρμονική ταλάντωση’.
    • Να προσδιορίζουν μέσω παραδειγμάτων τις έννοιες ‘περίοδος’, ‘συχνότητα’, ‘γωνιακή συχνότητα’.
    • Να διατυπώνουν τις μαθηματικές σχέσεις που συνδέουν τις παραπάνω έννοιες.
    • Να περιγράφουν την κίνηση ενός σώματος χρησιμοποιώντας τα χαρακτηριστικά γνωρίσματα της απλής αρμονικής ταλάντωσης.
    • Να κατανοήσουν τις έννοιες ‘απομάκρυνση’, ‘πλάτος’, ‘φάση’ σε σχέση με ένα σώμα που πραγματοποιεί απλή αρμονική ταλάντωση.
    • Να περιγράφουν τα είδη των κινήσεων που πραγματοποιεί ένα σώμα σε μια απλή αρμονική ταλάντωση στη διάρκεια μιας περιόδου.
    • Να διατυπώνουν μαθηματικά τη συνάρτηση της απομάκρυνσης με το χρόνο σε μια απλή αρμονική ταλάντωση.
    • Να σχεδιάζουν τη γραφική παράσταση της απομάκρυνσης σε σχέση με το χρόνο.
    • Να εντοπίζουν στη γραφική παράσταση απομάκρυνσης-χρόνου τα χωρία όπου το σώμα που ταλαντώνεται έχει θετική και αρνητική απομάκρυνση. Να υπολογίζουν από τη γραφική παράσταση απομάκρυνσης-χρόνου το πλάτος, την περίοδο, τη συχνότητα και τη γωνιακή συχνότητα.
    • Να διατυπώνουν μαθηματικά τη συνάρτηση της ταχύτητας με το χρόνο σε μια απλή αρμονική ταλάντωση.
    • Να σχεδιάζουν τη γραφική παράσταση της ταχύτητας σε σχέση με το χρόνο.
    • Να περιγράφουν τα είδη της κίνησης ενός σώματος που πραγματοποιεί απλή αρμονική ταλάντωση με βάση τη γραφική παράσταση ταχύτητας-χρόνου στη διάρκεια μιας περιόδου.
    • Να υπολογίζουν από τη γραφική παράσταση ταχύτητας - χρόνου το πλάτος, την περίοδο, τη συχνότητα και τη γωνιακή συχνότητα.
    • Να αποδεικνύουν αλγεβρικά και γραφικά ότι η διαφορά φάσης ταχύτητας και απομάκρυνσης είναι .
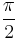    • Να διατυπώνουν μαθηματικά τη συνάρτηση της επιτάχυνσης με το χρόνο σε μια απλή αρμονική ταλάντωση.
    • Να σχεδιάζουν τη γραφική παράσταση της επιτάχυνσης σε σχέση με το χρόνο.
    • Να περιγράφουν τα είδη της κίνησης ενός σώματος που πραγματοποιεί απλή αρμονική ταλάντωση με βάση τη γραφική παράσταση επιτάχυνσης-χρόνου στη διάρκεια μιας περιόδου.
    • Να υπολογίζουν από τη γραφική παράσταση επιτάχυνσης-χρόνου το πλάτος, την περίοδο, τη συχνότητα και τη γωνιακή συχνότητα.
    • Να αποδεικνύουν αλγεβρικά και γραφικά ότι η διαφορά φάσης επιτάχυνσης - απομάκρυνσης είναι 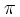και επιτάχυνσης – ταχύτητας είναι .
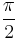    • Να διατυπώνουν μαθηματικά τη συνάρτηση της δύναμης επαναφοράς με το χρόνο σε μια απλή αρμονική ταλάντωση.
    • Να σχεδιάζουν τη γραφική παράσταση της δύναμης επαναφοράς σε σχέση με το χρόνο.
    • Να περιγράφουν τα είδη της κίνησης ενός σώματος που πραγματοποιεί απλή αρμονική ταλάντωση με βάση τη γραφική παράσταση δύναμης επαναφοράς-χρόνου στη διάρκεια μιας περιόδου.
    • Να υπολογίζουν από τη γραφική παράσταση δύναμης επαναφοράς - χρόνου το πλάτος, την περίοδο, τη συχνότητα και τη γωνιακή συχνότητα.
    • Να αποδεικνύουν αλγεβρικά και γραφικά ότι η διαφορά φάσης δύναμης επαναφοράς-απομάκρυνσης είναι 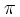, δύναμης επαναφοράς – ταχύτητας είναι 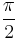και δύναμης επαναφοράς - επιτάχυνσης είναι μηδέν.
    • Να αναγνωρίζουν πότε η απομάκρυνση, η ταχύτητα, η επιτάχυνση και η δύναμη επαναφοράς είναι μηδέν και πότε μέγιστες.
    • Να κατανοήσουν το ρόλο της δύναμης επαναφοράς σε μια απλή αρμονική ταλάντωση.
    • Να προσδιορίσουν τη σταθερά επαναφοράς ως μέγεθος το οποίο εξαρτάται από τα φυσικά χαρακτηριστικά του συστήματος που ταλαντώνεται.
    • Να αποδεικνύουν για ένα σύστημα ότι η σχέση 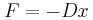αποτελεί ικανή συνθήκη για να πραγματοποιεί το σύστημα απλή αρμονική ταλάντωση.
    • Να εφαρμόζουν τη σχετική μεθοδολογία για να αποδεικνύουν ότι ένα σώμα πραγματοποιεί απλή αρμονική ταλάντωση.
    • Να σχεδιάζουν τη γραφική παράσταση της δύναμης επαναφοράς σε σχέση με την απομάκρυνση.
    • Να εντοπίζουν στη γραφική παράσταση δύναμης επαναφοράς – απομάκρυνσης τα χωρία όπου τα δύο μεγέθη παίρνουν θετικές και αρνητικές τιμές και να ερμηνεύουν τις απόψεις τους σε σχέση με το είδος της κίνησης που πραγματοποιεί το σώμα που ταλαντώνεται.
    • Να υπολογίζουν τη σταθερά επαναφοράς από τη γραφική παράσταση δύναμης επαναφοράς – απομάκρυνσης.
    • Να υπολογίζουν το έργο της δύναμης επαναφοράς από τη γραφική παράσταση δύναμης επαναφοράς – απομάκρυνσης.
    • Να σχεδιάζουν τη γραφική παράσταση της επιτάχυνσης σε σχέση με την απομάκρυνση.
    • Να εντοπίζουν στη γραφική παράσταση επιτάχυνσης – απομάκρυνσης τα χωρία όπου τα δύο μεγέθη παίρνουν θετικές και αρνητικές τιμές και να ερμηνεύουν τις απόψεις τους σε σχέση με το είδος της κίνησης που πραγματοποιεί το σώμα που ταλαντώνεται.
    • Να υπολογίζουν από τη γραφική παράσταση δύναμης επαναφοράς–απομάκρυνσης τη γωνιακή συχνότητα.
    • Να υπολογίζουν την περίοδο της απλής αρμονικής ταλάντωσης.
    • Να κατανοήσουν την εξάρτηση της περιόδου της απλής αρμονικής ταλάντωσης από την μάζα του ταλαντούμενου σώματος και από την σταθερά επαναφοράς του συστήματος.




  • Εισηγητής βιντεοδιαλέξεων: Χατζέλλης Ευάγγελος
    Επιστημονικός έλεγχος: Ζησιμόπουλος Γεώργιος

    Επιμέλεια ύλης σημειώσεων θεωρίας: Χατζέλλης Ευάγγελος
    Επιστημονικός έλεγχος: Ζησιμόπουλος Γεώργιος

    Σχεδιασμός και επιστημονική επιμέλεια applets: Παλόγος Αντώνιος, Στεφανίδης Κωνσταντίνος
    Ανάπτυξη: Λέτης Σταύρος

    Επιμέλεια υλικού θεμάτων προς επίλυση τύπου Α: Φωτεινάκης Γεώργιος, Χατζέλλης Ευάγγελος
    Επιστημονικός έλεγχος: Ζησιμόπουλος Γεώργιος, Στεφανίδης Κωνσταντίνος